 Μια σημαντική ερώτηση για την κοσμολογία σήμερα, είναι πόση μάζα περιέχεται στο Σύμπαν και ποιες οι επιπτώσεις της μάζας αυτής στην γεωμετρία και τον ρυθμό διαστολής του Σύμπαντος.
Μια σημαντική ερώτηση για την κοσμολογία σήμερα, είναι πόση μάζα περιέχεται στο Σύμπαν και ποιες οι επιπτώσεις της μάζας αυτής στην γεωμετρία και τον ρυθμό διαστολής του Σύμπαντος.1. Πόση ύλη περιέχει το Σύμπαν;
Αν δεν υπήρχε καθόλου μάζα στο Σύμπαν, αυτό θα διαστελλόταν για πάντα, και η ταχύτητα με την οποία θα απομακρύνονταν μεταξύ τους τα αντικείμενα που θα βρίσκονταν σε ακινησία ως προς το διαστελλόμενο σύμπαν, δεν θα μεταβαλλόταν καθώς το Σύμπαν θα επεκτεινόταν.
Γνωρίζουμε φυσικά ότι το Σύμπαν δεν είναι άδειο αλλά γεμάτο με ύλη και η συνηθισμένη ύλη έλκει άλλη ύλη μέσω των δυνάμεων βαρύτητας, προκαλώντας έτσι επιβράδυνση στη διαστολή του σύμπαντος.
Αν η πυκνότητα του σύμπαντος υπερβαίνει κάποιο συγκεκριμένο όριο, γνωστό ως κρίσιμη πυκνότητα, αυτή η βαρυτική έλξη θα είναι αρκετά ισχυρή ώστε να σταματήσει τη διαστολή και στη συνέχεια να την αντιστρέψει κάνοντας το Σύμπαν να καταρρεύσει τελικά στη μεγάλη σύνθλιψη.
Από την άλλη πλευρά, αν η μέση πυκνότητα του σύμπαντος είναι μικρότερη από την κρίσιμη πυκνότητα, το σύμπαν θα διαστέλλεται για πάντα, και μάλιστα μετά από κάποιο σημείο η διαστολή προχωρεί σαν να ήταν το σύμπαν άδειο από ύλη.
Ένα "κρίσιμο σύμπαν", με μια κρίσιμη πυκνότητα ισορροπεί μεταξύ αυτών των δύο δυνατοτήτων.

2. Γιατί να έχουμε ένα σύμπαν με κρίσιμη πυκνότητα;
Για αρκετό χρόνο πιστεύαμε ότι η πυκνότητα του σύμπαντός μας συμφωνεί με την κρίσιμη πυκνότητα αρκετά καλά (με διαφορά μικρότερη από ένα παράγοντα ίσο με 10.) Αν και το σφάλμα αυτό στη συμφωνία φαίνεται μεγάλο, είναι αξιοσημείωτη η συμφωνία. Το να επιτευχθούν αρχικές συνθήκες τέτοιες ώστε η μέση πυκνότητα να παραμείνει πολύ κοντά στην κρίσιμη τιμή για έστω και απειροελάχιστο χρονικό διάστημα, είναι σα να προσπαθεί κάποιος να ισορροπήσει ένα μολύβι στη μύτη του.
Ένα σύμπαν που θα είχε αρχικά μια πυκνότητα ελαφρά μικρότερη από την κρίσιμη, κάνει την πυκνότητα αυτή ακόμη μικρότερη από την κρίσιμη και σύντομα δεν διαφέρει από ένα σχεδόν άδειο σύμπαν.
Παρόμοια, μια έστω και λίγο μεγαλύτερη πυκνότητα από την κρίσιμη κάνει το σύμπαν να βρεθεί τάχιστα στην κατάσταση της μεγάλης σύνθλιψης, χωρίς να μπορέσει να φτάσε την ηλικία που γνωρίζουμε ότι έχει το σύμπαν μας – κάπου 13,5 δισεκατομμύρια χρόνια.
Για να πετύχουμε ένα σύμπαν όμοιο με το δικό μας πρέπει οι αρχικές συνθήκες πυκνότητας να έχουν συντονιστεί τόσο τέλεια ώστε να συμφωνούν με την κρίσιμη πυκνότητα με μια ακρίβεια περίπου 1 προς 1060!
Για αρκετό διάστημα θεωρούσαμε απλούστερο και αισθητικά ευχάριστο να δεχόμαστε αξιωματικά ότι το σύμπαν μας έχει ακριβώς την κρίσιμη πυκνότητα. Οι εκδοχές της πληθωριστικής θεωρίας που αναπτύχθηκαν στις αρχές της δεκαετίας του 1980 μας έδωσαν ένα μηχανισμό για να πάρουμε την κρίσιμη πυκνότητα για το σύμπαν σχεδόν με απεριόριστη ακρίβεια. Για πολλά χρόνια ένα ακριβώς κρίσιμο σύμπαν εθεωρείτο ως μια από τις σίγουρες προβλέψεις της πληθωριστικής θεωρίας.
3. Η γεωμετρία και η πυκνότητα του σύμπαντος
Στην Γενική Θεωρία της Σχετικότητας του Einstein που διατυπώθηκε το 1915, η βαρύτητα προσεγγίζεται με όρους της γεωμετρίας παρά ως μια ακόμη δύναμη. Η ύλη καθορίζει πως θα καμπυλωθεί ο χωροχρόνος, και η καμπύλωση του χωροχρόνου καθορίζει πως θα κινηθούν τα σώματα.
Για την ειδική περίπτωση ενός Σύμπαντος το οποίο επεκτείνεται, που το θεωρούμε γεμάτο με ομοιόμορφη πυκνότητα ύλης, και αποτελεί μια καλή προσέγγιση για τη μεγάλη κλίμακα, η γενική σχετικότητα προβλέπει μια διασύνδεση μεταξύ της πυκνότητας του σύμπαντος (συγκριτικά πάντα με την κρίσιμη πυκνότητα) και της γεωμετρίας του.
Ένα σύμπαν με κρίσιμη πυκνότητα (σε κάποιο σταθερό κοσμικό χρόνο) έχει τη γνωστή Ευκλείδεια γεωμετρία, η οποία μας είναι πολύ γνωστή από την καθημερινή μας εμπειρία και από την κλασσική προοπτική που διδάσκεται στη ζωγραφική. Ένα σύμπαν όμως με πυκνότητα μικρότερη ή μεγαλύτερη από την κρίσιμη δεν έχει Ευκλείδεια γεωμετρία -έχει υπερβολική γεωμετρία αν η πυκνότητα είναι μικρότερη από την κρίσιμη και σφαιρική αν η πυκνότητα είναι μεγαλύτερη από την κρίσιμη.
Στις μικρές κλίμακες αυτές οι διαφορετικές γεωμετρίες μοιάζουν πολύ. Ένα μυρμήγκι στην επιφάνεια ενός μήλου θα αντιλαμβανόταν το άμεσο περιβάλλον του ως τελείως επίπεδο και θα δυσκολευόταν να διαπιστώσει ότι το μήλο είναι κυρτό. Παρόμοια αν η καμπυλότητα του Σύμπαντος γινόταν εμφανής μόνο σε κλίμακες αρκετών δισεκατομμυρίων ετών φωτός θα μπορούσαμε να καταλήξουμε στην απατηλή αίσθηση ότι το σύμπαν μας είναι επίπεδο και η γεωμετρία του Ευκλείδεια. Μόνο στις πολύ μεγάλες κλίμακες, – μεγαλύτερες από τη λεγόμενη κλίμακα καμπυλότητας – οι διαφορές μεταξύ των γεωμετριών θα έδιναν σημαντικά αποτελέσματα ώστε να παρατηρηθούν.
Τα τρία παρακάτω σχήματα δείχνουν τις διαφορές που εμφανίζονται κατά την παρατήρηση μακρινών αντικειμένων (προοπτική) στην υπερβολική, την Ευκλείδεια και τη σφαιρική γεωμετρία. Και στις τρεις περιπτώσεις ο χώρος διαιρείται σε όμοια κελιά των οποίων οι ακμές δείχνονται με ράβδους. Οι σφαίρες εντός των κελιών έχουν όμοιο μέγεθος και η αυξανόμενη απόστασή τους παριστάνεται με προοδευτικό χρωματισμό με κόκκινο χρώμα.

Στην Ευκλείδεια γεωμετρία ο χώρος διαιρείται σε κύβους, και κανείς αντιλαμβάνεται τη συνηθισμένη προοπτική: το φαινόμενο γωνιακό μέγεθος των αντικειμένων είναι αντιστρόφως ανάλογο με την απόστασή τους

Στην υπερβολική γεωμετρία ο χώρος γεμίζει μόνο αν υποδιαιρεθεί σε δωδεκάεδρα. Στον ευκλείδειο χώρο ένα τέτοιο γέμισμα είναι αδύνατο. Το μέγεθος των κελιών εδώ είναι της ίδιας τάξης με την κλίμακα καμπυλότητας. Αν και η προοπτική των κοντινών αντικειμένων στον υπερβολοειδή χώρο είναι αρκετά όμοια με αυτή του ευκλείδειου χώρου, το φαινόμενο γωνιακό μέγεθος των μακρινών αντικειμένων μειώνεται πολύ πιο γρήγορα, στην πραγματικότητα εκθετικά όπως φαίνεται και στην εικόνα.
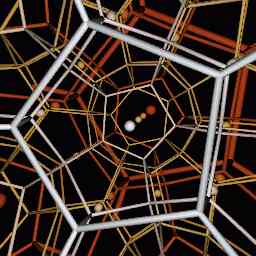
Ο σφαιρικός χώρος που φαίνεται στην ανωτέρω εικόνα, γεμίζει επίσης με κανονικά δωδεκάεδρα. Η γεωμετρία του σφαιρικού χώρου μοιάζει με την επιφάνεια της γης εκτός από το γεγονός ότι στην περίπτωσή μας θεωρούμε μια τρισδιάστατη σφαίρα αντί για μια δισδιάστατη. Η προοπτική στον σφαιρικό χώρο είναι ιδιόμορφη. Καθώς αυξάνεται η απόσταση, τα αντικείμενα πρώτα εμφανίζονται να μικραίνουν (όπως στον Ευκλείδειο χώρο), φτάνουν ένα ελάχιστο, και τελικά εμφανίζονται να μεγαλώνουν ξανά με την αύξηση της απόστασης. Η συμπεριφορά αυτή οφείλεται στην δυνατότητα της σφαιρικής γεωμετρίας να προκαλεί εστίαση των ακτίνων.
4. Ποιά γεωμετρία έχει το Σύμπαν μας;
Κατά τη δεκαετία του 1980 οι παρατηρήσεις ήταν αρκετά ατελείς και αυτό μας έκανε να νομίζουμε ότι το Σύμπαν είχε την κρίσιμη πυκνότητα. Οι πιο πρόσφατες όμως παρατηρήσεις μας είναι όλο και πιο δύσκολο να συμβιβαστούν με την κρίσιμη πυκνότητα.
Είναι γνωστό ότι εκτός από την ύλη που φωτοβολεί και αποτελεί τα άστρα, το σύμπαν περιέχει μια μεγάλη ποσότητα "σκοτεινής ύλης", ιδιαίτερα στην περιοχή που αποτελεί την άλω των γαλαξιών. Συμπεραίνουμε την παρουσία της από τη βαρυτική έλξη που ασκεί στην ύλη με την οποία γειτονεύει. Επειδή η σκοτεινή ύλη κατανέμεται χωρίς να σχηματίζει τα έντονα συμπυκνώματα που σχηματίζει η ορατή, φωτεινή ύλη, η φαινόμενη μέση πυκνότητα μοιάζει να αυξάνει όλο και περισσότερο καθώς κοιτάζουμε σε ολοένα και μεγαλύτερες κλίμακες. Για αρκετό χρόνο πιστεύαμε ότι ερευνώντας σε αρκετά μεγάλη κλίμακα θα αποκαλύπταμε κάποια κρίσιμη πυκνότητα της σκοτεινής ύλης.
Σήμερα φαίνεται ότι μια τέτοια ελπίδα δεν θα πραγματοποιηθεί. Σήμερα είναι δυνατόν να ερευνήσουμε τη μέση πυκνότητα του σύμπαντος σε κλίμακες αρκετά μεγάλες ώστε να αποτελούν ένα ικανοποιητικό δείγμα του σύμπαντος. Θεωρούμε την "αναλογία της συμπυκνωμένης ύλης βαρυονίων" σαν μια ισχυρή ένδειξη υπέρ ενός σύμπαντος με πυκνότητα μικρότερη από την κρίσιμη. Σμήνη πλούσια σε γαλαξίες, είναι τα μεγαλύτερα συστήματα του σύμπαντος που συγκρατούνται με βαρυτικές δυνάμεις. Αν και σπάνια, αυτά τα συστήματα είναι θαυμάσια εργαστήρια για να μελετήσουμε τη σύνθεση της ύλης που γεμίζει το σύμπαν.
Χρησιμοποιώντας πυρηνική φυσική βρίσκουμε την πυκνότητα του σύμπαντος σε βαρυόνια. Με την πυκνότητα της βαρυονικής ύλης γνωστή, μπορούμε να καθορίσουμε την ολική πυκνότητα μετρώντας την αναλογία των βαρυονίων.
Η βαρυονική μάζα ενός σμήνους μπορεί να βρεθεί προσθέτοντας τις μάζες των γαλαξιών που αποτελούν το σμήνος -τις οποίες πάλι συμπεραίνουμε από το φως τους – με τη μάζα του θερμού αερίου νέφους μεταξύ των γαλαξιών του σμήνους – την οποία βρίσκουμε από παρατηρήσεις ακτίνων Χ εκπεμπόμενες από το αέριο νέφος.
Η ολική μάζα μπορεί να βρεθεί με διάφορες μεθόδους. Οι κινήσεις των γαλαξιών του σμήνους, μας επιτρέπουν να καθορίσουμε το βάθος που έχει το "φρέαρ δυναμικού" της βαρύτητας και κατ’ επέκταση η συνολική μάζα που δημιουργεί αυτό το δυναμικό.
Παρατηρήσεις ακτίνων Χ μας επιτρέπουν να μετρήσουμε τη μάζα των διαγαλαξιακών αερίων, ενώ αξιοποιούμε και την εστιακή δυνατότητα της βαρύτητας του σμήνους, επί του φωτός αντικειμένων που βρίσκονται πίσω από το σμήνος. Αυτή η δράση του σμήνους ως βαρυτικού φακού προκαλεί παραμόρφωση των ειδώλων των αντικειμένων που βρίσκονται πίσω από το σμήνος. Η μέθοδος αυτή λοιπόν μας δίνει μια εντελώς ανεξάρτητη εκτίμηση για την συνολική μάζα.
Οι τεχνικές αυτές καθώς και άλλες ανεξάρτητες τεχνικές, υποδηλώνουν ένα Σύμπαν με πυκνότητα ίση περίπου με το 1/3 της κρίσιμης πυκνότητας. Αν και ένα Σύμπαν με πυκνότητα ίση με την κρίσιμη δεν μπορεί ακόμα να αποκλειστεί τελείως, η πιθανότητα να έχουμε την κρίσιμη πυκνότητα μοιάζει σήμερα μικρή.
5. Συμβιβάζοντας ένα Σύμπαν χαμηλής πυκνότητας με την πληθωριστική θεωρία.
Αν το Σύμπαν έχει πράγματι πυκνότητα κάτω της κρίσιμης, σημαίνει άραγε αυτό ότι πρέπει να εγκαταλείψουμε την ιδέα του πληθωρισμού; Αν ένα επίπεδο σύμπαν είναι αυτό που προβλέπει η θεωρία του πληθωρισμού τότε θα πρέπει να εγκαταλείψουμε την ιδέα του πληθωρισμού.
Ωστόσο υπάρχει τρόπος να ξεφύγουμε από αυτό το δίλημμα. Ο πληθωρισμός μέσα σε μια μεμονωμένη φυσαλίδα μπορεί να δημιουργήσει ένα ομαλό σύμπαν με υπερβολική γεωμετρία, όπως ακριβώς απαιτείται για ένα σύμπαν με πυκνότητα μικρότερη της κρίσιμης.
Ο ανοιχτός πληθωρισμός σε μεμονωμένες φυσαλίδες, βασίστηκε στις ιδέες του S. Coleman, F. de Luccia και του J.R. Got στις αρχές της δεκαετίας του 1980, και αναπτύχθηκε παραπέρα στα μέσα της δεκαετίας του 1990 από τους M. Bucher, A.S. Goldhaber, και N. Turok και αργότερα από τους M. Sasaki, T. Tanaka, και K. Yamamoto.
Ο πληθωρισμός εξομαλύνει το σύμπαν καθώς παραδέχεται μια αρχική εποχή του όπου συνέβη πολύ γρήγορη επέκταση, κατά τη διάρκεια της οποίας εξαλείφθηκαν οποιεσδήποτε ανωμαλίες υπήρχαν πριν από τον πληθωρισμό. Στη συνηθισμένη θεωρία πληθωρισμού, όπως αναπτύχθηκε από τους Guth, Linde, Albrecht, και Steinhardt, αυτή η εξομάλυνση έκανε επίσης το Σύμπαν επίπεδο δημιουργώντας τελικά ένα σύμπαν με κρίσιμη πυκνότητα. Στο συνηθισμένο πληθωρισμό, ένα κρίσιμο σύμπαν θα μπορούσε κατ’ αρχή να αποφευχθεί αν ο πληθωρισμός ήταν μικρότερος, αλλά στην περίπτωση αυτή η εξομάλυνση σε πολύ μεγάλη κλίμακα θα παρέμενε ένα μυστήριο, που θα έκανε τη θεωρία του πληθωρισμού να χάσει αρκετή από την ελκυστικότητά της.
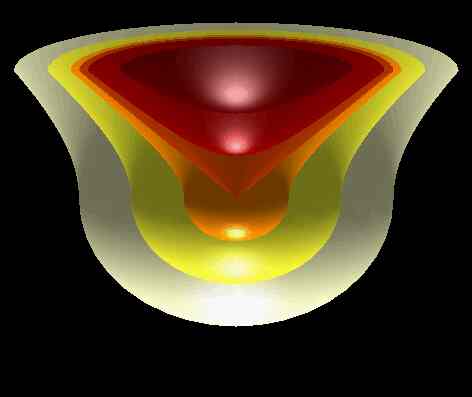
Η δημιουργία ενός ανοιχτού Σύμπαντος εντός μεμονωμένης φυσαλίδας. Η κάθετη διεύθυνση δείχνει τον χρόνο και οι οριζόντιες κατευθύνσεις είναι χωρικές κατευθύνσεις. Η τιμή του πεδίου inflaton είναι σταθερή στις διάφορες τομές και τα χρώματα δείχνουν την ψύξη του σύμπαντος καθώς κανείς περνάει στο εσωτερικό της φυσαλίδας. Η φυσαλίδα διαστέλλεται μέσα στον περιβάλλοντα χωροχρόνο ο οποίος διαστέλλεται πληθωριστικά παγιδευμένη μέσα στο ψευδο-κενό. Εμείς ζούμε στο εσωτερικό της φυσαλίδας.
Στον ανοιχτό πληθωρισμό μεμονωμένης φυσαλίδας υπάρχουν δύο εποχές πληθωρισμού. Στον πληθωρισμό ο ρυθμός της διαστολής ελέγχεται από ένα βαθμωτό πεδίο, γνωστό ως πεδίο inflaton. Το πεδίο inflaton θέλει να βρεθεί στον πυθμένα του φρέατος δυναμικού κυλώντας στα τοιχώματα του φρέατος, και καθώς το πεδίο κατεβαίνει ο ρυθμός της επέκτασης του σύμπαντος ελαττώνεται, και προοδευτικά τερματίζεται η εποχή του πληθωρισμού. Στον ανοιχτό πληθωρισμό, το πεδίο inflaton, αρχικά παραμένει παγιδευμένο σε ένα τοπικό ελάχιστο του δυναμικού. Ενώ το πεδίο βρίσκεται σ’ αυτό το ελάχιστο, μια πρώτη εποχή πληθωριστικής διαστολής συμβαίνει, κατά τη διάρκεια της οποίας το σύμπαν εξομαλύνεται. Πράγματι κατά τη διάρκεια αυτής της εποχής η συμμετρία του χωροχρόνου είναι τόσο μεγάλη ώστε καμιά ιδιαίτερη κατεύθυνση του χρόνου δεν προτιμάται από οποιαδήποτε άλλη. Βλέπε το παρακάτω σχήμα.
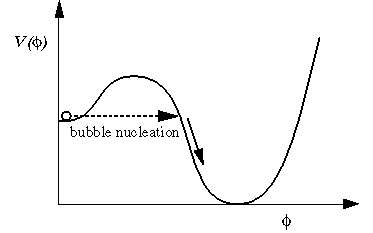
Σύμφωνα με την κλασσική φυσική, αν το πεδίο inflaton παγιδευτεί στο τοπικό ελάχιστο δεν μπορεί να διαφύγει ποτέ. Στην κβαντομηχανική όμως, επιτρέπεται το πεδίο να περάσει μέσα από το φράγμα δυναμικού με το φαινόμενο σήραγγας. Αυτό το φαινόμενο σήραγγας συμβαίνει μέσω της δημιουργίας φυσαλίδας, η οποία διαστέλλεται, όπως περίπου διαστέλλεται μια φυσαλίδα μέσα σ’ ένα δοχείο με νερό που βράζει.
Στη συνέχεια η φυσαλίδα διαστέλλεται με την ταχύτητα του φωτός. Δεν μπορεί να έχει καμιά άλλη ταχύτητα από την ταχύτητα του φωτός, γιατί αλλιώς θα έπρεπε να υπάρχει μια προτιμητέα κατεύθυνση του χρόνου. Οι επιφάνειες στο εσωτερικό της φυσαλίδας, επί των οποίων το βαθμωτό πεδίο έχει σταθερή τιμή έχουν μια χωρική γεωμετρία υπερβολοειδή, και αυτές είναι οι επιφάνειες τις οποίες εμείς που ζούμε εντός της φυσαλίδας αντιλαμβανόμαστε ως επιφάνειες με σταθερή τιμή του κοσμικού χρόνου. Καθώς κανείς περνάει μέσα στη φυσαλίδα, το εσωτερικό συνεχίζει να διαστέλλεται πληθωριστικά, δημιουργώντας ένα σύμπαν με τεράστια ακτίνα καμπυλότητας. Ακόμα, στο εσωτερικό της φυσαλίδας, η ενέργεια του πεδίου inflaton μετατρέπεται σε συνηθισμένη ύλη και ακτινοβολία, και το υπερβολοειδές σύμπαν συνεχίζει να διαστέλλεται και να ψύχεται.
6. Πως μπορούμε να ελέγξουμε τον ανοιχτό πληθωρισμό;
Η καλύτερη ελπίδα μας για να ελέγξουμε τον ανοιχτό πληθωρισμό είναι να μετρήσουμε τη γεωμετρία του σύμπαντος, πράγμα που μπορεί να γίνει με παρατήρηση των διακυμάνσεων της κοσμικής μικροκυματικής ακτινοβολίας.
Η μικροκυματική ακτινοβολία υποβάθρου αντιστοιχεί σε ακτινοβολία μέλανος σώματος θερμοκρασίας 3οΚ και είναι το απομεινάρι μιας εποχής περίπου 300.000 χρόνων μετά το Big Bang, όταν το σύμπαν είχε μέγεθος περίπου το ένα χιλιοστό του σημερινού. Εκείνη την εποχή τα ηλεκτρόνια, εξαιτίας της ψύξης του σύμπαντος ενώνονταν με τα πρωτόνια και άλλους πυρήνες και σχημάτιζαν ουδέτερα άτομα υδρογόνου και άλλων στοιχείων. Εξαιτίας του περάσματος από μια κατάσταση σχεδόν πλήρους ιονισμού σε μια κατάσταση ουδέτερου αερίου, το σύμπαν που μέχρι τότε ήταν αδιαφανές στην ακτινοβολία έγινε διαφανές. Οι ανομοιομορφίες στην ακτινοβολία υποβάθρου μας δίνουν ένα στιγμιότυπο των διακυμάνσεων εκείνης της περιόδου, οι οποίες αργότερα μεταβλήθηκαν σε γαλαξίες και στις άλλες δομές που παρατηρούμε σήμερα.
Πηγή
